二叉树的最大路径和

路径被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

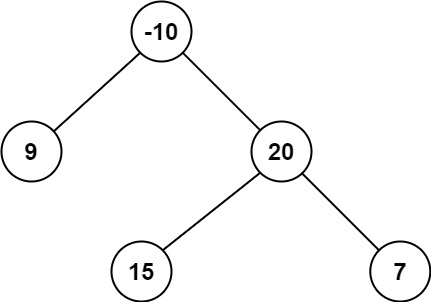
输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

代码实现：

class Solution {
    int maxSum = Integer.MIN_VALUE;

    public int maxPathSum(TreeNode root) {
        maxGain(root);
        return maxSum;
    }

    public int maxGain(TreeNode node) {
        if (node == null) {
            return 0;
        }
        
        // 递归计算左右子节点的最大贡献值
        // 只有在最大贡献值大于 0 时，才会选取对应子节点
        int leftGain = Math.max(maxGain(node.left), 0);
        int rightGain = Math.max(maxGain(node.right), 0);

        // 节点的最大路径和取决于该节点的值与该节点的左右子节点的最大贡献值
        int priceNewpath = node.val + leftGain + rightGain;

        // 更新答案
        maxSum = Math.max(maxSum, priceNewpath);

        // 返回节点的最大贡献值
        return node.val + Math.max(leftGain, rightGain);
    }
}

建树

在笔试题中，需要自己根据数组建树。数组的形式不同，有两种建树方式。

递归法：三叉树

public static Node buildTree(int[] tree, int idx){
    if(tree[idx] == -1){
        return null;
    }
    Node root = new Node(tree[idx]);
    if(idx * 3 + 1 < tree.length){
        root.left = buildTree(tree, idx * 3 + 1);	//二叉树将3改为2，并少一个if语句
    }
    if(idx * 3 + 2 < tree.length){
        root.middle = buildTree(tree, idx * 3 + 2);
    }
    if(idx * 3 + 3 < tree.length){
        root.right = buildTree(tree, idx * 3 + 3);
    }
    return root;
}

该方法需要数组非常的完整，对于null节点的左右节点，仍然需要在数组中用null表示，否则数组长度不够会导致建的树不完整。

层序遍历

public static Node buildTree(int[] nums){
    Node root = new Node(nums[0]);
    Queue<Node> queue = new ArrayDeque<>();	//利用队列先进先出的特性
    queue.offer(root);
    int idx = 1;
    while(!queue.isEmpty() && idx < nums.length){
        int size = queue.size();
        for(int i = 0; i < size; i++){
            Node node = queue.peek();
            queue.poll();
            if(idx < nums.length && nums[idx] != -1){
                node.left = new Node(nums[idx]);
                queue.offer(node.left);
            }else{
                node.left = null;
            }
            idx++;
            if(idx < nums.length && nums[idx] != -1){	//二叉树少一个if语句
                node.middle = new Node(nums[idx]);
                queue.offer(node.middle);
            }else{
                node.middle = null;
            }
            idx++;
            if(idx < nums.length && nums[idx] != -1){
                node.right = new Node(nums[idx]);
                queue.offer(node.right);
            }else{
                node.right = null;
            }
            idx++;
        }
    }
    return root;
}

该方法的数组不需要将null节点的子节点表示出来。

三叉树的最大路径和

对于笔试题的三叉树，只需将上两步融合。

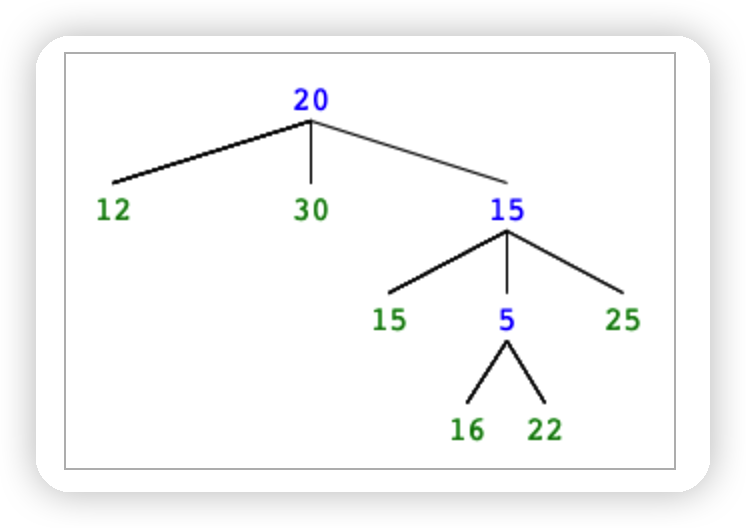
输入：
19
20 12 30 15 -1 -1 -1 -1 -1 -1 15 5 25 -1 -1 -1 16 -1 22
其中，-1表示空节点
输出：
92

代码实现：

import java.util.*;

class Node{
    int val;
    Node left;
    Node middle;
    Node right;

    public Node(int val){
        this.val = val;
    }
}

public class Main{
    public static void main(String[] args){
       Scanner sc = new Scanner(System.in);
       int n = sc.nextInt();
       int[] tree = new int[n];
       for(int i = 0; i < n; i++){
           tree[i] = sc.nextInt();
       }
       Node root = buildTree(tree);
       maxGain(root);
       System.out.println(maxSum);
    }

    public static int maxSum = Integer.MIN_VALUE;
    public static int maxGain(Node node){
        if(node == null){
            return 0;
        }
        int leftGain = Math.max(maxGain(node.left), 0);
        int middleGain = Math.max(maxGain(node.middle), 0);
        int rightGain = Math.max(maxGain(node.right), 0);
        int price = node.val + Math.max(leftGain + middleGain, Math.max(middleGain + rightGain, leftGain + rightGain));
        maxSum = Math.max(maxSum, price);
        return node.val + Math.max(Math.max(leftGain, middleGain), rightGain);
    }

    public static Node buildTree(int[] nums){
        Node root = new Node(nums[0]);
        Queue<Node> queue = new ArrayDeque<>();
        queue.offer(root);
        int idx = 1;
        while(!queue.isEmpty() && idx < nums.length){
            int size = queue.size();
            for(int i = 0; i < size; i++){
                Node node = queue.peek();
                queue.poll();
                if(idx < nums.length && nums[idx] != -1){
                    node.left = new Node(nums[idx]);
                    queue.offer(node.left);
                }else{
                    node.left = null;
                }
                idx++;
                if(idx < nums.length && nums[idx] != -1){
                    node.middle = new Node(nums[idx]);
                    queue.offer(node.middle);
                }else{
                    node.middle = null;
                }
                idx++;
                if(idx < nums.length && nums[idx] != -1){
                    node.right = new Node(nums[idx]);
                    queue.offer(node.right);
                }else{
                    node.right = null;
                }
                idx++;
            }
        }
        return root;
    }
}

参考

LeetCode官方题解

jiankychen教你学算法 - 学算法，看我就够了