LeetCode 494.目标和

目标和

给你一个整数数组 nums 和一个整数 target 。

向数组中的每个整数前添加 '+' 或 '-' ，然后串联起所有整数，可以构造一个 表达式 ：

• 例如，nums = [2, 1] ，可以在 2 之前添加 '+' ，在 1 之前添加 '-' ，然后串联起来得到表达式 "+2-1" 。

返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。

输入：nums = [1,1,1,1,1], target = 3
输出：5
解释：一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3

0 - 1背包

算法思路：

要使表达式结果为target，可将式子分为加法部分plus和减法部分neg，根据neg = sum - plus和plus - neg = target可得，plus = (target + sum) / 2。问题就转化为装满容量为plus的背包，有几种方法（组合问题）。

1. 循环前进行前置判断。当target + sum不能被二整除，以及plus < 0时，没有方案，返回0。

   if((target + sum) % 2 != 0 || (target + sum) < 0)return 0;

2. 确定dp数组以及下标的含义

   dp[j]表示，填满j（包括j）这么大容积的包，有dp[j]种方法。

3. 确定递推公式

   不考虑nums[i]的情况下，填满容量为j的背包，有dp[j]种方法。

   那么考虑nums[i]的话（只要搞到nums[i]），凑成dp[j]就有dp[j - nums[i]] 种方法。

   例如：dp[j]，j 为5，
   
   已经有一个1（nums[i]） 的话，有 dp[4]种方法 凑成 dp[5]。
   已经有一个2（nums[i]） 的话，有 dp[3]种方法 凑成 dp[5]。
   已经有一个3（nums[i]） 的话，有 dp[2]中方法 凑成 dp[5]
   已经有一个4（nums[i]） 的话，有 dp[1]中方法 凑成 dp[5]
   已经有一个5（nums[i]）的话，有 dp[0]中方法 凑成 dp[5]
   那么凑整dp[5]有多少方法呢，也就是把 所有的 dp[j - nums[i]] 累加起来。

   所以求组合类的公式，都是类似dp[j] += dp[j - nums[i]]。

4. dp数组初始化

   dp[0] = 1，装满容量为0的背包，有1种方法，就是装0件物品。

5. 确定遍历顺序

   先遍历物品nums[i]，再遍历背包j。

6. 举例推导dp数组

   

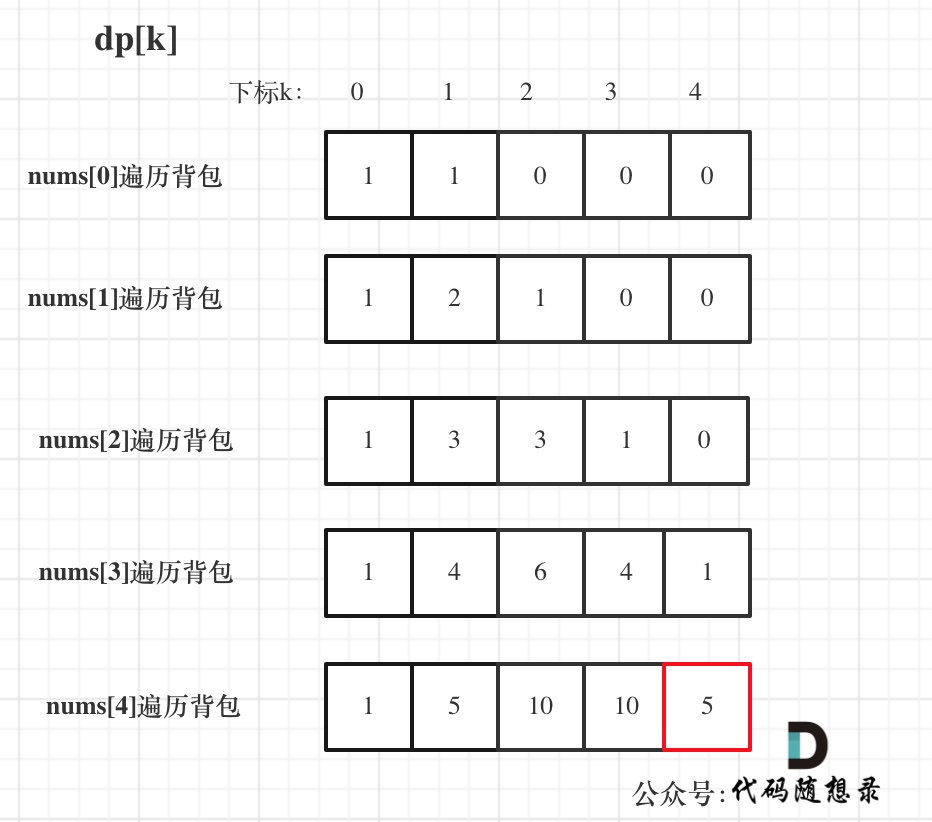
代码实现：

class Solution {
    public int findTargetSumWays(int[] nums, int target) {
        int sum = 0;
        for(int num: nums){
            sum += num;
        }
        if((target + sum) % 2 != 0 || (target + sum) < 0)return 0;
        int plus = (target + sum) / 2;
        int[] dp = new int[plus + 1];
        dp[0] = 1;
        for(int i = 0; i < nums.length; i++){
            for(int j = plus; j >= nums[i]; j--){
                dp[j] += dp[j - nums[i]];
            }
        }
        return dp[plus];
    }
}

参考

代码随想录 - 目标和