组合总和

给你一个无重复元素的整数数组candidates和一个目标整数target，找出candidates中可以使数字和为目标数target的所有不同组合，并以列表形式返回。你可以按任意顺序返回这些组合。

candidates中的同一个数字可以无限制重复被选取。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于150个。

输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。

方法一：回溯

算法思路：

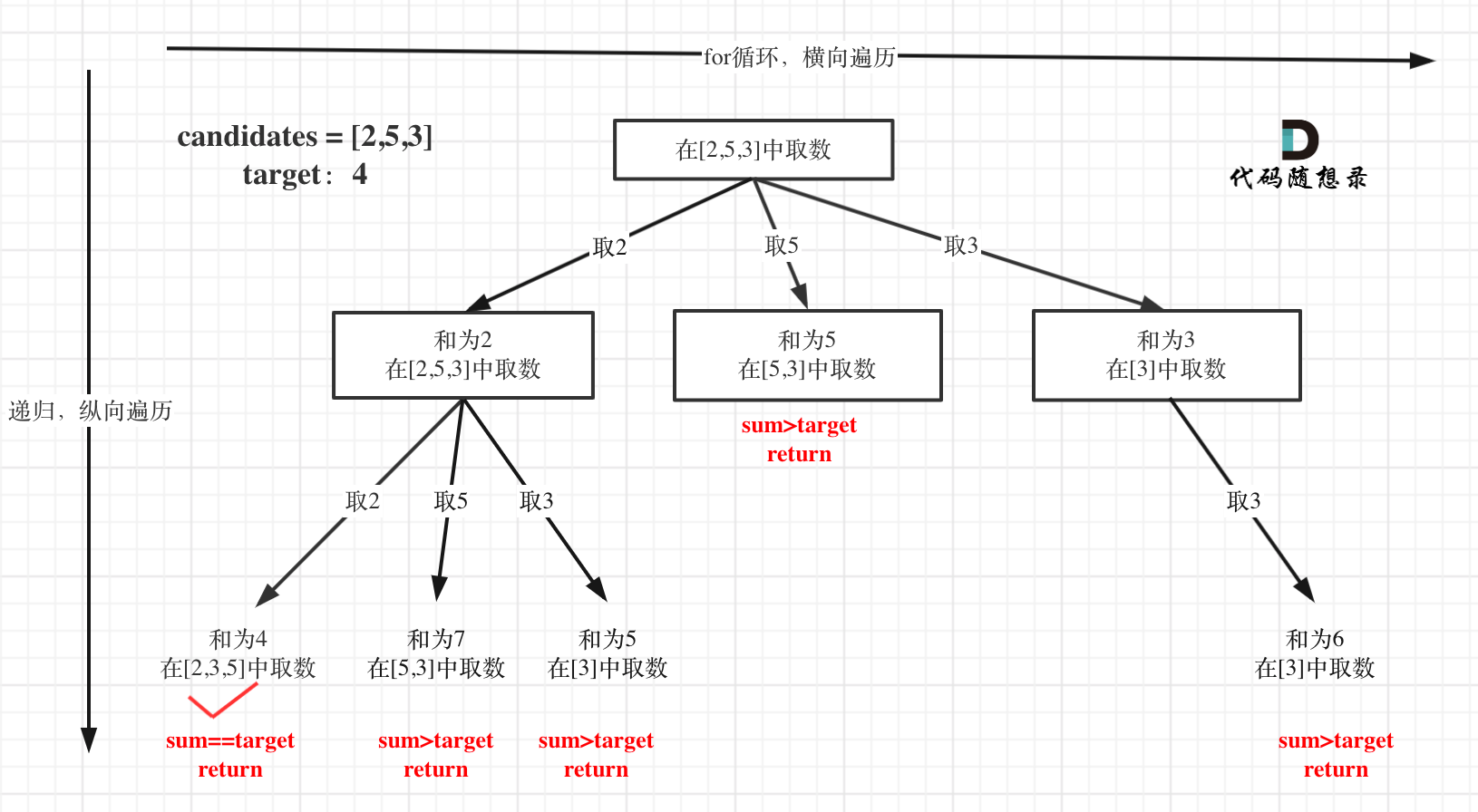
本题和77.组合 (opens new window)，216.组合总和III (opens new window)和区别是：本题没有数量要求，可以无限重复，但是有总和的限制，所以间接的也是有个数的限制。

确定递归函数的返回值以及参数

除了题中输入candidates和target外，还需要定义sum来记录path中的总和。

startIndex的设置（仅针对求组合问题，排列问题不一样）：
- 如果是一个集合来求组合的话，就需要startIndex，如77.组合 (opens new window)，216.组合总和III (opens new window)。
- 如果是多个集合取组合，各个集合之间相互不影响，就不需要设置startIndex，如17.电话号码的字母组合

确定终止条件

当sum大于等于target时终止递归，当sum等于target时，将path添加到result中。

if(sum >= target){
      if(sum == target){
          result.add(new ArrayList<>(path));
      }
      return;
}

单层搜索的过程

单层for循环依然是从startIndex开始，搜索candidates集合。此处需要注意元素可以重复选取。

for(int i = startIndex; i < candidates.length; i++){
            sum += candidates[i];
            path.add(candidates[i]);
            backTracking(candidates, target, sum, i);//可以重复选取元素，所以不用i+1
            sum -= candidates[i];
            path.removeLast();
        }

代码实现：

class Solution {
    public List<List<Integer>> result = new ArrayList<>();
    public LinkedList<Integer> path = new LinkedList<>();

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        backTracking(candidates, target, 0, 0);
        return result;
    }

    public void backTracking(int[] candidates, int target, int sum, int startIndex){
        if(sum >= target){
            if(sum == target){
                result.add(new ArrayList<>(path));
            }
            return;
        }

        for(int i = startIndex; i < candidates.length; i++){
            sum += candidates[i];
            path.add(candidates[i]);
            backTracking(candidates, target, sum, i);
            sum -= candidates[i];
            path.removeLast();
        }
    }
}

方法二：剪枝优化

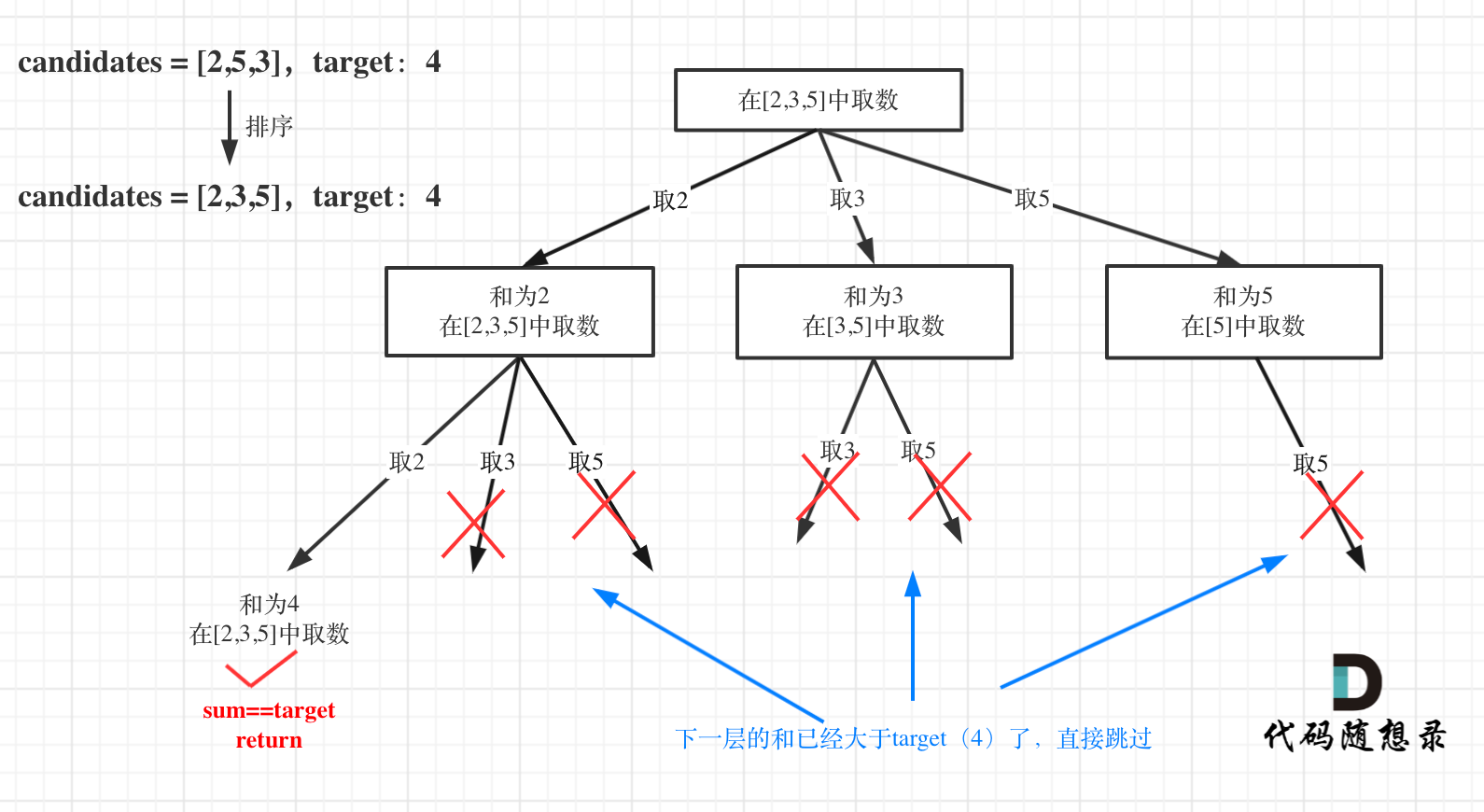
对于排序数组candidates，当sum + candidates[i] > target时，后续的数就不需要遍历了，直接break。

代码实现：

class Solution {
    public List<List<Integer>> result = new ArrayList<>();
    public LinkedList<Integer> path = new LinkedList<>();

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        Arrays.sort(candidates);		//排序
        backTracking(candidates, target, 0, 0);
        return result;
    }

    public void backTracking(int[] candidates, int target, int sum, int startIndex){
        
        if(sum == target){
            result.add(new ArrayList<>(path));
            return;
        }
        

        for(int i = startIndex; i < candidates.length; i++){
            if(sum + candidates[i] > target){
                break;				//若超出范围，则跳出循环
            }
            sum += candidates[i];
            path.add(candidates[i]);
            backTracking(candidates, target, sum, i);
            sum -= candidates[i];
            path.removeLast();
        }
    }
}

参考

代码随想录 - 组合总和