组合

LeetCode 77.组合

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按任何顺序返回答案。

输入：n = 4, k = 2
输出：
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

方法一：回溯

算法思路：

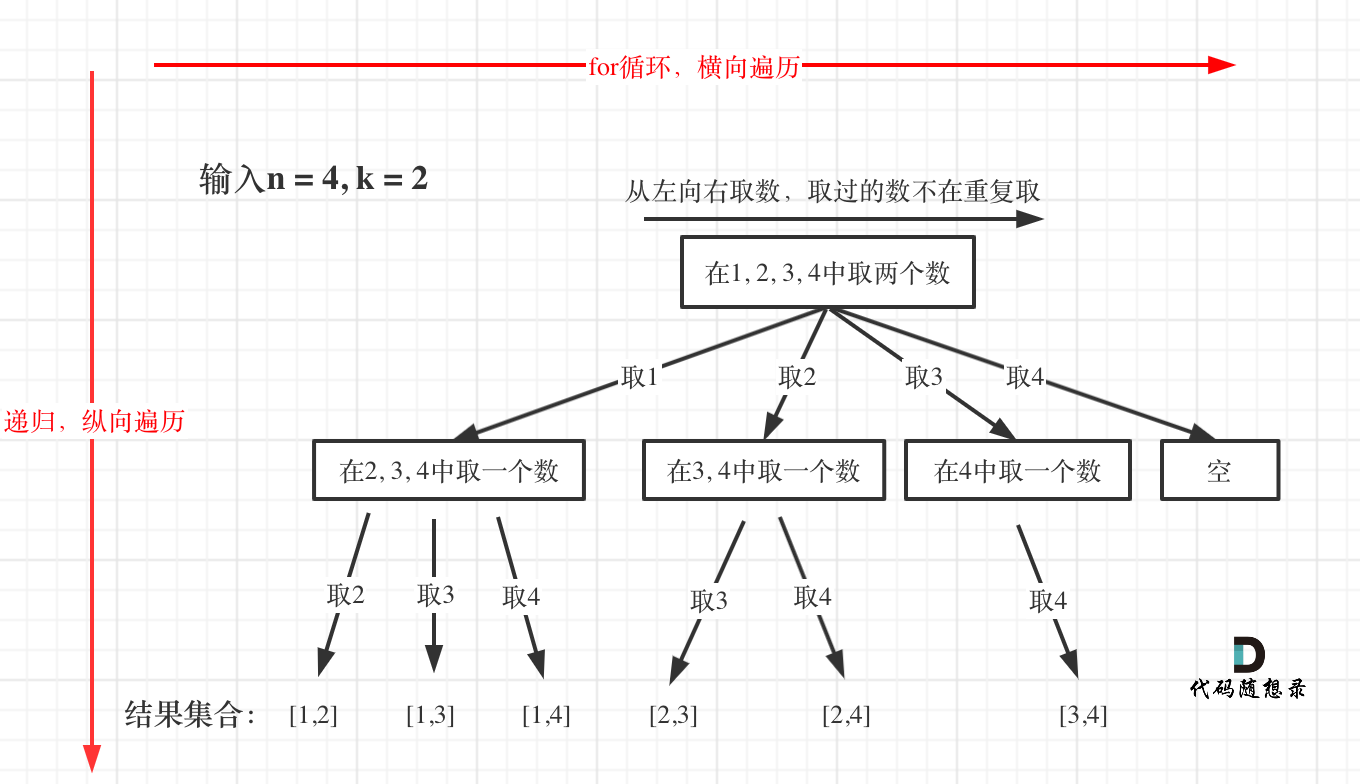
  1. 确定递归函数的返回值以及参数

    除了n与k，我们还需要设置变量startIndex，用来记录本层递归中，集合从哪里开始遍历。如，在取完1后，下一层递归就要在[2, 3, 4]中取数。

  2. 回溯函数的终止条件

    当到达叶子节点时停止递归，即path数组的大小达到k。此时，用二维数组result将path保存起来，终止本层递归。

    if(path.size() == k){
    		result.add(new ArrayList<>(path));
    		return;
    }

  3. 单层搜索的过程

    for循环用来横向遍历，递归的过程是纵向遍历。for循环每次从startIndex开始遍历，然后用path保存取到的节点。

    for(int i = startIndex; i <= n; i++){
                path.add(i);//将当前位置节点放入path中
                backTracking(n, k, i + 1);//递归：进入下一层遍历，注意搜索要从i+1开始
                path.removeLast();//回溯，撤销处理的节点
    }

代码实现：

class Solution {
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();

    public List<List<Integer>> combine(int n, int k) {
        backTracking(n, k, 1);
        return result;
    }

    public void backTracking(int n, int k, int startIndex){
        if(path.size() == k){
            result.add(new ArrayList<>(path));
            return;
        }

        for(int i = startIndex; i <= n; i++){
            path.add(i);
            backTracking(n, k, i + 1);
            path.removeLast();
        }
    }
}

方法二：剪枝优化

如果在起始位置之后的元素个数全部加入到path中也达不到k，那就没必要搜索了。

  • 已经选择的元素个数：path.size()

  • 还需要的元素个数：k - path.size()

  • 在集合n中的最后起始位置：n - (k - path.size()) + 1

    例：n = 4, k = 3, 目前已选取0，n - (k - path.size()) + 1 = 2，最晚从2开始搜索，得[2,3,4]

for(int i = startIndex; i <= n - (k - path.size()) + 1; i++)

参考

代码随想录 - 组合